The mathematics that will be introduced involves the calculus of variations, Hamiltonian formulations of the Euler-Lagrange equations, bifurcation theory, numerical methods for ODE two-point boundary value problems (including numerical symmetry breaking), and the theory of the second variation in isoperimetric calculus of variations problems.
We start with a description of the mechanics model, known as the Cosserat theory of rods, and the quaternion parameterization of proper rotation matrices. We then describe the mathematical methods, and finally we discuss how to fit the parameters of our model to describe DNA itself, and make some computations.
The sum total of all this material will occupy several weeks.
Throughout the course Roman indices will be assumed to run through the values 1, 2 and 3 with repeated indices summed, unless the context or text indicates otherwise.
These orthonormality relations mean exactly that the ![]() cosine
matrix
cosine
matrix ![]() of components of the three vectors
of components of the three vectors ![]() with respect to any fixed (right handed) system of orthonormal basis vectors,
say
with respect to any fixed (right handed) system of orthonormal basis vectors,
say ![]() ,
is a proper rotation matrix (i.e. a rotation matrix with determinant
,
is a proper rotation matrix (i.e. a rotation matrix with determinant ![]() )
or (a representative of) an element of the group
)
or (a representative of) an element of the group ![]() .
.
Notice that the frame ![]() is defined externally to the curve
is defined externally to the curve ![]() ,
i.e. the frame contains additional information to the centerline. Thus
the
,
i.e. the frame contains additional information to the centerline. Thus
the ![]() frame has a different status from say the Frenet-Serret frame which is
made up from the tangent, normal and binormal to the curve, and which is
defined by the curve
frame has a different status from say the Frenet-Serret frame which is
made up from the tangent, normal and binormal to the curve, and which is
defined by the curve ![]() and its derivatives.
and its derivatives.
The curve ![]() should be thought of as the centerline of the rod (say the average of the
two backbones in the case of DNA) while the frame
should be thought of as the centerline of the rod (say the average of the
two backbones in the case of DNA) while the frame ![]() should be regarded as specifying the orientation of each cross-section
of the rod (or say some smooth interpolation of the orientation of each
set of base pairs in the case of DNA).
should be regarded as specifying the orientation of each cross-section
of the rod (or say some smooth interpolation of the orientation of each
set of base pairs in the case of DNA).
The parameter ![]() will be given a precise physical interpretation in a little while, but
is, roughly speaking, distance along the centerline of the rod.
will be given a precise physical interpretation in a little while, but
is, roughly speaking, distance along the centerline of the rod.
As the ![]() are an orthonormal basis they satisfy kinematic equations of the form
are an orthonormal basis they satisfy kinematic equations of the form
-------------------------------
It is a simple exercise (do it!) to derive the existence of the
vector ![]() ,
which is sometimes called the Darboux vector.
,
which is sometimes called the Darboux vector.
(Hint for one way: because the triad ![]() is a basis at each
is a basis at each ![]() there
exist functions
there
exist functions ![]() such that
such that ![]() .
Differentiating the orthonormality conditions on the
.
Differentiating the orthonormality conditions on the ![]() then
give conditions on the
then
give conditions on the ![]() which imply that there are only three independent non-zero
which imply that there are only three independent non-zero ![]() ,
and they have the property that they are equivalent to taking a vector
cross-product, i.e. the Darboux vector exists.)
,
and they have the property that they are equivalent to taking a vector
cross-product, i.e. the Darboux vector exists.)
-------------------------------
We also introduce the components of the Darboux vector ![]() with respect to the basis
with respect to the basis ![]() through
through
The components ![]() determine the frame
determine the frame ![]() (up to a single arbitrary rotation specifying initial conditions for the
frame) through integration of the (nine, scalar) differential equations
(up to a single arbitrary rotation specifying initial conditions for the
frame) through integration of the (nine, scalar) differential equations
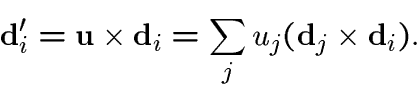
Once the frame ![]() is known, the three component
is known, the three component ![]() determine
the centerline
determine
the centerline ![]() (up to a single arbitrary translation specifying initial conditions on
the centerline) through integration of the equations
(up to a single arbitrary translation specifying initial conditions on
the centerline) through integration of the equations
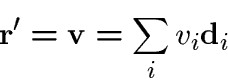
Thus the six scalar functions ![]() and
and ![]() ,
determine the configuration of the rod up to a single arbitrary rigid body
motion (i.e. a translation plus a rotation).
,
determine the configuration of the rod up to a single arbitrary rigid body
motion (i.e. a translation plus a rotation).
For this reason the six functions ![]() and
and ![]() can, and will, be called a set of strains for the rod.
can, and will, be called a set of strains for the rod.
There is certainly quite some arbitrariness in the definitions of
the strains, which arises from an arbitrariness in the relation of the
frame ![]() ,
and the parameter
,
and the parameter ![]() ,
to the material making up the rod.
,
to the material making up the rod.
We will usually assume the reference state to be a minimum energy or unstressed configuration (the precise definitions of which will arise later).
Usually (but not necessarily) the parameter ![]() is chosen to be arc-length along the centerline of the reference curve
is chosen to be arc-length along the centerline of the reference curve ![]() ,
in which case the reference strains satisfy
,
in which case the reference strains satisfy

Usually (but not necessarily) the reference unit vector field ![]() is chosen to be parallel to the tangent vector to the reference centerline
is chosen to be parallel to the tangent vector to the reference centerline ![]() so that provided
so that provided ![]() has been chosen to be arc-length in the reference state, we have for all
has been chosen to be arc-length in the reference state, we have for all ![]() that
that

In this situation the ![]() -components
of the strains are distinguished from the
-components
of the strains are distinguished from the ![]() and
and ![]() components, and it makes sense to describe
components, and it makes sense to describe ![]() and
and ![]() as shear strains, and (somewhat imprecisely)
as shear strains, and (somewhat imprecisely) ![]() as a stretch. Similarly
as a stretch. Similarly ![]() and
and ![]() are described as bending strains, while
are described as bending strains, while ![]() will be described as the twist (strain).
will be described as the twist (strain).
Here are some examples of typical strains:

As a matter of physical modelling, when interpreting mathematical
rod models as an approximation of long slender deformable bodies, it is
implicitly assumed that the whole three-dimensional shape of the body can
be reconstructed to a good approximation from knowledge of the centerline
and the frame, using a known, locally-defined reconstruction rule at each
value of the parameter ![]() .
.
For example, in the context of DNA it is implicitly assumed that
the location of each atom making up the ![]() th
base pair can be well-approximated once the frame, and centerline at the
arc-length corresponding to the
th
base pair can be well-approximated once the frame, and centerline at the
arc-length corresponding to the ![]() th
base are known.
th
base are known.
The arbitrariness in the choice of reference strains ![]() and
and ![]() can be regarded as an arbitrariness in the definition of the local reconstruction
rule, but once a reference configuration, or equivalently a local reconstruction
rule at each value of
can be regarded as an arbitrariness in the definition of the local reconstruction
rule, but once a reference configuration, or equivalently a local reconstruction
rule at each value of ![]() ,
has been set, then the same local reconstruction rule is used in any configuration
of the rod.
,
has been set, then the same local reconstruction rule is used in any configuration
of the rod.
For this to be a reasonable approximation, it is implicit assumed that the differences between the strains in any physically relevant configuration and in the reference configuration, are quite small, and for this reason rod theory is sometimes described as a linearized or small strain theory.
However this does not mean that the differences in configurations
are small, because small differences in strains over a relatively large
distance ![]() can give big differences in both centerline and frame. In particular rod
theory keeps full geometrical nonlinearities.
can give big differences in both centerline and frame. In particular rod
theory keeps full geometrical nonlinearities.
In an inextensible, unshearable rod, the strains ![]() in any configuration equal the strains
in any configuration equal the strains ![]() in the reference configuration, i.e. they satisfy the constraints
in the reference configuration, i.e. they satisfy the constraints
For an inextensible, unshearable rod it almost always makes sense
to choose the parameter ![]() to be arc-length in the reference configuration, because it is then also
arc-length in any configuration.
to be arc-length in the reference configuration, because it is then also
arc-length in any configuration.
Similarly it almost always makes sense to choose the reference framing
to be adapted so that ![]() ,
and
,
and
In fact for an inextensible, unshearable rod the configuration space
can be viewed as a centerline ![]() parametrized by arc-length
parametrized by arc-length ![]() ,along
with a single unit vector field,
,along
with a single unit vector field, ![]() say, which is everywhere orthogonal to the centerline
say, which is everywhere orthogonal to the centerline ![]() .
.
In other words a ribbon.
An orthonormal (adapted) right handed triad can then be constructed from any configuration of a ribbon from the definitions
Even for an inextensible, unshearable rod, with an adapted framing,
there remains some freedom as to which adapted frame is best chosen as
the reference configuration. This is a topic that will be of some importance
in our modelling of DNA, and we will return to it later.