The stresses exerted by the material
on one side of the cross-section at s acting on the material on the other
side of the cross-section can be averaged to yield a net force ![]() (of
the material on the side
(of
the material on the side ![]() acting on the material on the side
acting on the material on the side![]() ).
).
There is an arbitrary sign convention here, and as long as it is treated consistently it doesn't matter which convention you take.
Similarly the first moment of the stresses
acting across the cross-section can be averaged to yield a net moment ![]() (taken with the same sign convention as
(taken with the same sign convention as ![]() ).
).
As before ![]() and
and ![]() denote vectors, while
denote vectors, while ![]() and
and![]() will denote components of these vectors with respect to the variable basis
will denote components of these vectors with respect to the variable basis ![]() .
.
It will be of importance to recall the
elementary fact that because the frame ![]() is not constant, the component of the derivative
is not constant, the component of the derivative ![]() is not the derivative of the component
is not the derivative of the component![]() .
Rather using the kinematics of the basis
.
Rather using the kinematics of the basis ![]() ,
it can be seen that there is an additional cross-product term. Explicitly
,
it can be seen that there is an additional cross-product term. Explicitly
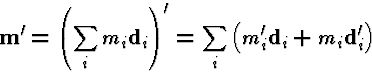
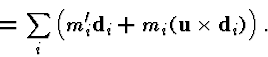
or
so that the ![]() th
component of
th
component of ![]() is the derivative of the
is the derivative of the ![]() th
component plus the
th
component plus the ![]() th
component of the cross-product
th
component of the cross-product![]() .
The coordinate free equilibrium equations are:
.
The coordinate free equilibrium equations are:
and
where ![]() is a distributed external force acting on the rod, and
is a distributed external force acting on the rod, and ![]() is a distributed external torque acting on the rod.
is a distributed external torque acting on the rod.
For the most part we will assume that
the external force and torque loadings vanish. But possible interesting
case would be weight due to a gravitational field, or a distributed force
loading arising from self-contact of the rod. That is the rod at arc-length ![]() touches (and pushes) the rod at arc-length
touches (and pushes) the rod at arc-length ![]() .
.
When selecting definitions of strains and stresses, it is important i) that the strains fully determine the configuration of the system, ii) the stresses allow a full determination of the balance laws, iii) the strains determine the stresses.
However in the constitutive model it is perfectly possible that the stresses could depend upon, for example, time derivatives of the strains (which are called viscous or plastic models), or time history of the strains (memory effect models), or space derivatives of the strains (which are called strain-gradient models).
Here we shall consider exclusively the case where the stresses are related to the strains through an algebraic constitutive relation, i.e. no derivatives or integrals of any type. In fact this assumption is precisely our definition of the model being elastic.
We first give some examples of simple elastic constitutive relations, and (somewhat) later discuss how general the constitutive relations might reasonably be, and how reasonable the simple choices might be.
The choice of appropriate constitutive relations is one of the most crucial issues in using rod models to describe physical phenomena.
In the case of modelling DNA the issue is (in my opinion) not at all well understood.
Perhaps the simplest choice of constitutive relation is a diagonal, linear (or at least affine) one. For each i (with no sum)
Here, as before, the ![]() and
and ![]() are prescribed functions of s determining the reference shape. And the
are prescribed functions of s determining the reference shape. And the![]() and
and ![]() are prescribed functions, which for reasons we shall see later, are usually
assumed to be strictly positive.
are prescribed functions, which for reasons we shall see later, are usually
assumed to be strictly positive.
Because of the form of the shift in the constitutive relations
we see that the stresses in the reference state vanish, i.e. the reference state is unstressed.
More generally for positive coefficients ![]() and
and ![]() the stress-strain law can be inverted (here trivially) to yield
the stress-strain law can be inverted (here trivially) to yield
In particular, invertibility implies (among other things) that when the reference state is stress-free it is the only unstressed state.
We will also use the fact that the constitutive
laws are hyper-elastic, which means precisely that there is a scalar-valued
function![]() of the six strains with the property that the constitutive relations can
be written in the form of partial derivatives of
of the six strains with the property that the constitutive relations can
be written in the form of partial derivatives of ![]()

The linear diagonal constitutive laws described above are hyper-elastic with the quadratic strain-energy density function
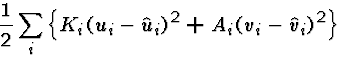
The elastic energy of the rod with strains ![]() and
and ![]() can be defined as
can be defined as
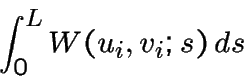
and ![]() is called the strain-energy density function.
is called the strain-energy density function.
In the diagonal, linearly elastic case we can see that the unstressed reference configuration is also the unique minimum energy configuration.
Much of the time we will be concerned
with the case of inextensible, unshearable elastic rods. As discussed earlier
the inextensibility and unshearability conditions are expressed by specifying
the values of the strains ![]() to always be their reference values
to always be their reference values ![]() (which
are usually assumed to be the triple
(which
are usually assumed to be the triple ![]() ).
).
For such rods the force![]() is a basic unknown, with no related constitutive relation, while the bending
and twist strains
is a basic unknown, with no related constitutive relation, while the bending
and twist strains ![]() and components of the moments
and components of the moments ![]() are
still related through constitutive relations, for example of the affine
form:
are
still related through constitutive relations, for example of the affine
form:
where the ![]() and the
and the ![]() are as before. We will also talk about hyper-elastic, inextensible, unshearable
rods. For the affine constitutive relation on the previous page, the elastic
strain energy of the rod is
are as before. We will also talk about hyper-elastic, inextensible, unshearable
rods. For the affine constitutive relation on the previous page, the elastic
strain energy of the rod is

plus some combination of constitutive relations, or unshearability or inextensibility constraints.
In fact when the balance laws are written
in terms of components wrt the frame ![]() ,
they (apparently) decouple from the kinematic equations.
,
they (apparently) decouple from the kinematic equations.
Balance laws become a closed system
of 6 first-order ODE
after six of the twelve quantities ![]() ,
, ![]() ,
, ![]() and
and ![]() are eliminated using the constitutive relations
are eliminated using the constitutive relations
(if the rod is inextensible and unshearable
the unknowns ![]() must be three of the variables retained).
must be three of the variables retained).
Resulting equations are nonlinear with
quadratic nonlinearities (because the constitutive relations were assumed
to be linear). When the constitutive laws are homogeneous (or autonomous)
i.e. have no explicit ![]() dependence, it is possible to find simple (and not so simple) closed form
solutions of the balance laws, and then with known strains to integrate
the kinematic equations to find explicit expressions for the associated
centerline and director frame. See Exercise Session 1. In general, both
for non-homogeneous and homogeneous constitutive relations, it is necessary
to solve the system numerically. Particularly because a typical rod problem
involves two-point boundary conditions, i.e. some of the variables are
given specified variables at
dependence, it is possible to find simple (and not so simple) closed form
solutions of the balance laws, and then with known strains to integrate
the kinematic equations to find explicit expressions for the associated
centerline and director frame. See Exercise Session 1. In general, both
for non-homogeneous and homogeneous constitutive relations, it is necessary
to solve the system numerically. Particularly because a typical rod problem
involves two-point boundary conditions, i.e. some of the variables are
given specified variables at ![]() ,
and some at
,
and some at ![]() say. It should be recalled (or realized) that the numerical solution of
initial value problems, i.e. problems where all the unknowns have specified
values at one value of the independent variable
say. It should be recalled (or realized) that the numerical solution of
initial value problems, i.e. problems where all the unknowns have specified
values at one value of the independent variable ![]() (usually
(usually ![]() ),
for smooth equations such as the above, and on a bounded interval, is essentially
trivial given todays computers and knowledge of algorithms. In contrast
the numerical solution of two-point boundary value problems is still nontrivial
(although of course the appropriate numerical methods are for the most
part very well understood). The other important observation is that even
though the balance laws, and the kinematic equations appear to naturally
decouple, the boundary conditions typically do not decouple, so that there
is effectively little simplification. For example perhaps the simplest
boundary value problem for an elastic rod is the strut, where with a standard
fixed basis
),
for smooth equations such as the above, and on a bounded interval, is essentially
trivial given todays computers and knowledge of algorithms. In contrast
the numerical solution of two-point boundary value problems is still nontrivial
(although of course the appropriate numerical methods are for the most
part very well understood). The other important observation is that even
though the balance laws, and the kinematic equations appear to naturally
decouple, the boundary conditions typically do not decouple, so that there
is effectively little simplification. For example perhaps the simplest
boundary value problem for an elastic rod is the strut, where with a standard
fixed basis ![]() of
of ![]() ,the
appropriate boundary conditions are
,the
appropriate boundary conditions are
These do not reduce to an initial value
problem for the stress components ![]() and
and ![]() because to know the components
because to know the components ![]() given
the boundary condition
given
the boundary condition ![]() it would be necessary to know the relation between the directors
it would be necessary to know the relation between the directors ![]() and the basis vectors
and the basis vectors ![]() .
Thus the problem is implicitly coupled. (We remark parenthetically that
the boundary conditions
.
Thus the problem is implicitly coupled. (We remark parenthetically that
the boundary conditions
do lead to a decoupled system for the stress components. This is a physically interesting, much studied problem with a so-called follower load. Its full solution behaviour is actually much more complicated than the strut.) Another physically interesting set of boundary conditions that we will study in our preparation for modelling DNA are
which have no boundary conditions whatsoever on the stress components.
Note that for an inextensible rod, there
can be no solution for![]()