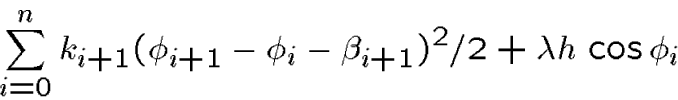
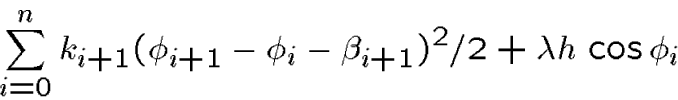
The quadratic terms are a model for the
energy stored in ![]() rotational springs, with spring constant
rotational springs, with spring constant ![]() at the
at the ![]() th
joint,
th
joint, ![]() and
a minimum energy at the
and
a minimum energy at the ![]() th
joint when the angles satisfy
th
joint when the angles satisfy
The fact that ![]() is prescribed is analogous to the boundary condition
is prescribed is analogous to the boundary condition ![]() in the continuous problem, while the ``boundary condition'' involving
in the continuous problem, while the ``boundary condition'' involving ![]() is a discretized version of the vanishing moment condition
is a discretized version of the vanishing moment condition ![]() ,
which says that there is no moment applied at the top of the segment with
,
which says that there is no moment applied at the top of the segment with ![]() th
joint.
th
joint.
We could equally well eliminate ![]() and
and ![]() using the boundary conditions to leave a sum with index range
using the boundary conditions to leave a sum with index range ![]() with
with ![]() unknowns (and redefining
unknowns (and redefining ![]() )
and there would be only
)
and there would be only ![]() quadratic terms to be summed.
quadratic terms to be summed.
The term in the energy involving ![]() and
and ![]() models the potential energy of a vertical load (with the convention
models the potential energy of a vertical load (with the convention ![]() +ve acting downward) applied to the
+ve acting downward) applied to the ![]() st
joint (or equivalently the end of the
st
joint (or equivalently the end of the ![]() th
segment with each segment being of length
th
segment with each segment being of length ![]() ).
Think of a bucket of water of weight
).
Think of a bucket of water of weight ![]() hung from the
hung from the ![]() st
joint, then the potential energy is just the height
st
joint, then the potential energy is just the height ![]() times the weight
times the weight ![]() .
.
In the formulation where ![]() is kept as a variable it seems a little strange that the load is not applied
at the tip of the
is kept as a variable it seems a little strange that the load is not applied
at the tip of the ![]() st
segment, but it is quite usual that in a finite difference approximation,
it is necessary to introduce an additional mesh point `beyond the boundary'
in order to approximate derivative boundary conditions at the boundary.
In any case, in this example eliminating
st
segment, but it is quite usual that in a finite difference approximation,
it is necessary to introduce an additional mesh point `beyond the boundary'
in order to approximate derivative boundary conditions at the boundary.
In any case, in this example eliminating ![]() eliminates any confusion.
eliminates any confusion.
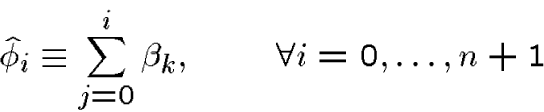
Thus we can see that the ![]() can be identified as determining a piece-wise constant approximation of
the unstressed strain
can be identified as determining a piece-wise constant approximation of
the unstressed strain ![]() in the continuous problem, or equivalently the
in the continuous problem, or equivalently the ![]() determine a piece-wise linear approximation with corner values
determine a piece-wise linear approximation with corner values ![]() ,
of the continuous unstressed shape
,
of the continuous unstressed shape ![]() determined
by the property
determined
by the property ![]() .
.
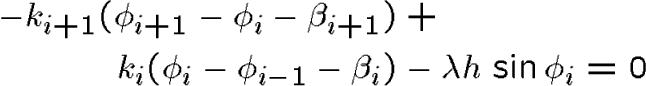
which is a set of ![]() nonlinear equations for the
nonlinear equations for the ![]() unknowns
unknowns ![]() ,
, ![]() ,
but the equations also contain many additional parameters, namely the single
scalars
,
but the equations also contain many additional parameters, namely the single
scalars ![]() and
and ![]() and the sets of parameters
and the sets of parameters ![]() ,
, ![]() and
and ![]() ,
, ![]() .
.
Notice that the boundary condition relating ![]() to
to ![]() is exactly the additional first-order condition that is obtained by taking
the partial derivative with respect to the variable
is exactly the additional first-order condition that is obtained by taking
the partial derivative with respect to the variable ![]() .
This is the finite dimensional manifestation of what is called natural
boundary conditions in the calculus of variations (which we will see in
a little while).
.
This is the finite dimensional manifestation of what is called natural
boundary conditions in the calculus of variations (which we will see in
a little while).
The boundary condition is actually implied
by the variational principle. In contrast it makes no sense to take a partial
derivative with respect to the variable ![]() because the boundary condition gives
because the boundary condition gives ![]() a definite value in terms of the given parameter
a definite value in terms of the given parameter ![]() .
Such boundary conditions are sometimes called imposed, and are not implied
by the variational principle.
.
Such boundary conditions are sometimes called imposed, and are not implied
by the variational principle.
These equations could have been derived
directly as the balance (about the ![]() th
joint) of moments acting on the
th
joint) of moments acting on the ![]() th
segment. Thus we see that there is a variational formulation or minimization
principle giving the moment balance equations. Notice that following common
practice we talk about a minimization principle, but the balance law comes
as the first-order stationary condition of all partial derivatives vanishing
(i.e. the potential is only known to be flat, but it could be a local minimum,
a local maximum, or some sort of saddle point).
th
segment. Thus we see that there is a variational formulation or minimization
principle giving the moment balance equations. Notice that following common
practice we talk about a minimization principle, but the balance law comes
as the first-order stationary condition of all partial derivatives vanishing
(i.e. the potential is only known to be flat, but it could be a local minimum,
a local maximum, or some sort of saddle point).
It is certainly of considerable interest
to know which of all the equilibria (solutions of the balance laws) are
actually local minima (which we expect to be stable equilibria). The type
of the critical point can be classified by studying the second derivative
of the potential evaluated at a particular critical point.
For the particular potential above, the
matrix is tri-diagonal with a typical ![]() block centred on the
block centred on the ![]() entry
being
entry
being
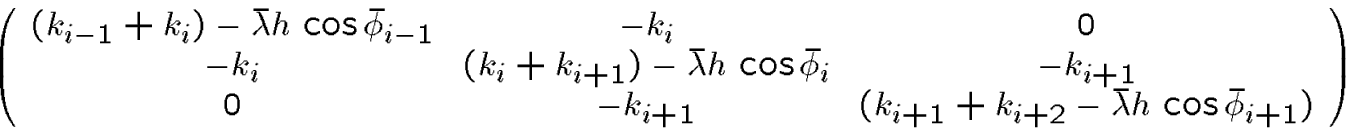
and appropriately modified first and last
blocks (after ![]() and
and ![]() are eliminated using the boundary conditions).
are eliminated using the boundary conditions).
Here ![]() is a particular solution of the equilibrium conditions with
is a particular solution of the equilibrium conditions with ![]() at which the second derivative (or second variation) is being computed.
The dependence of the second derivative on the the solution
at which the second derivative (or second variation) is being computed.
The dependence of the second derivative on the the solution ![]() is particularly simple because the bending part of the energy is exactly
quadratic.
is particularly simple because the bending part of the energy is exactly
quadratic.
Similarly because the terms involving the ![]() in an expansion of the energy are all linear in the
in an expansion of the energy are all linear in the ![]() the parameters
the parameters ![]() do not appear explicitly in the second derivative (although the
do not appear explicitly in the second derivative (although the ![]() certainly appear explicitly in the first-order conditions, and so implicitly
in the second derivative through the exact form of the equilibrium
certainly appear explicitly in the first-order conditions, and so implicitly
in the second derivative through the exact form of the equilibrium ![]() ).
Because the second derivative matrix is symmetric, it has only real eigenvalues,
and we will call the solution,
).
Because the second derivative matrix is symmetric, it has only real eigenvalues,
and we will call the solution, ![]() non-degenerate
if its second derivative matrix is nonsingular, i.e. is not an eigenvalue
of the matrix.
non-degenerate
if its second derivative matrix is nonsingular, i.e. is not an eigenvalue
of the matrix.
For non-degenerate equilibria we define its index to be the number of negative eigenvalues of its second derivative matrix. In particular a Taylor series expansion of the (finite dimensional) potential shows that a non-degenerate equilibrium is a local minimum of the potential (and thus presumably stable) precisely if its index is zero.
We remark that classifying degenerate equilibria is more subtle, because the second derivative cannot be used to bound all the higher order terms. (Similarly in infinite dimensional problems the situation is not so straightforward even at non-degenerate equilibria.)
The exercise sessions will ask you to compute
the second derivative at some particular solutions in the case ![]() .
.
In a little while we will turn to discussing
how the above discrete system, can be interpreted as a discretization of
the continuous system which will be recovered in a limit ![]() ,
, ![]() .
But first we will discuss methods for solving nonlinear systems of parameter-dependent
algebraic equations, and understanding typical behaviours.
.
But first we will discuss methods for solving nonlinear systems of parameter-dependent
algebraic equations, and understanding typical behaviours.
Generally speaking it is hopeless to find anything other than very special solutions of nonlinear equations analytically, and we must instead turn to numerical methods.
Because we know that our problem has an associated variational formulation, we could implement a numerical method exploiting that structure, say steepest descent, i.e. take an iterative method that at each step marches down the gradient of the potential. Such methods have some very desirable features. For example they can reasonably be expected to converge to a local minimum of the potential from an essentially arbitrary starting point--which is an extremely powerful statement.
On the other hand minimization by steepest descent or other methods has its draw backs, for example often there is slow convergence in the neighbourhood of a local minimum. For our purposes the bigest disadvantage of minimization methods is that they can only be expected to find local minima, and as we shall see it can be rather instructive to find other types of (presumably unstable) equilibria.
The only practical alternative to a minimization method is a root-finding technique applied directly to the system of equations that arises as the first-order necessary conditions. If for the moment we freeze all parameters in the first-order conditions, the first-order conditions assume the general form
At this level of generality the only practical
way to solve such systems numerically is some sort of iterative method
starting from a sufficiently good guess for the solution. Amongst such
iterative schemes, those that are some variant of Newton's method are extremely
powerful.
Neglecting the higher order terms, and
using the fact that by assumption ![]() ,
we see that the next iterate
,
we see that the next iterate ![]() defined via
defined via
Newton's method had two major potential
difficulties. First it may be either computationally expensive or difficult
to solve the linear system for the update ![]() either because the matrix
either because the matrix ![]() is very large and dense, or is ill-conditioned or actually singular. Second,
to start the iteration you need a first guess
is very large and dense, or is ill-conditioned or actually singular. Second,
to start the iteration you need a first guess ![]() ,
and often that guess has to be really quite good in order that the Newton
iteration will converge.
,
and often that guess has to be really quite good in order that the Newton
iteration will converge.
Our particular problem has special features
that can help with both of these potential difficulties. First because
we have a variational principle we know that the first order conditions
are of the form ![]() ,
but with the vector field
,
but with the vector field ![]() equal to the gradient of the scalar potential,
equal to the gradient of the scalar potential, ![]() say.
say.
Thus ![]() .
In particular the Jacobian matrix is just the symmetric matrix of second
derivatives of the potential
.
In particular the Jacobian matrix is just the symmetric matrix of second
derivatives of the potential ![]() ,
which for the planar rod problem is tri-diagonal (some such banded sparsity
structure of the Jacobian is typical of problems that arise as discretizations
of systems of ordinary differential equations). Linear systems involving
banded matrices can be solved extremely efficiently (for example a banded
Gaussian elimination), whenever they are not singular.
,
which for the planar rod problem is tri-diagonal (some such banded sparsity
structure of the Jacobian is typical of problems that arise as discretizations
of systems of ordinary differential equations). Linear systems involving
banded matrices can be solved extremely efficiently (for example a banded
Gaussian elimination), whenever they are not singular.
The second special feature that we shall
exploit is the parameter dependence of the problem with an explicitly known
solution at one parameter value (namely the unstressed shape when ![]() ).
We shall apply parameter continuation methods in our numerical computations
of rod equilibria.
).
We shall apply parameter continuation methods in our numerical computations
of rod equilibria.
Let us make this outline more concrete. Suppose therefore that we have a system of equations of the form
How might we compute such a branch of solutions?
If we seek solutions for ![]() with
with ![]() small, we can expand the solution as
small, we can expand the solution as
But ![]() as
as ![]() is known to be a solution, and (as a matter of notation)
is known to be a solution, and (as a matter of notation) ![]() is just the Jacobian
is just the Jacobian ![]() .
Thus we see that by ignoring
.
Thus we see that by ignoring ![]() terms we obtain a nonhomogeneous linear system that can be solved for a
unique solution
terms we obtain a nonhomogeneous linear system that can be solved for a
unique solution ![]() provided that the Jacobian
provided that the Jacobian ![]() is nonsingular:
is nonsingular:
Accordingly we can reasonably expect that
for ![]() small a Newton iterative solve of the equations at the parameter value
small a Newton iterative solve of the equations at the parameter value ![]() will converge if we take as initial guess
will converge if we take as initial guess
Once the Newton iterate has converged, and if the Jacobian is nonsingular at the new solution, we may repeat the process to generate a new initial guess at another nearby value of the parameter.
Thus we can generate a number of solutions
at a discrete set of values of the parameter ![]() that are close to each other, and which approximate the branch of solutions
that are close to each other, and which approximate the branch of solutions ![]() through
the initially known solution
through
the initially known solution ![]() .
.
This is an elementary (and rather naive) description of numerical continuation. As you can probably imagine there is a wealth of important detail in getting the method to work efficiently, but the above captures at least the flavour of the method that is implemented in the continuation code AUTO that we will use later on (via the graphics interface VBM).
We can see that the above method is problematic
whenever we hit a solution with a singular or near singular Jacobian. The
analysis of what happens at such singular points is the domain of bifurcation
theory. The typical behaviour at simple singular points is that the branch
of solutions persists, but there may be multiple branches of solutions,
or there may be a fold point at which the parameter ![]() has
a local extreme value along the branch of solutions.
has
a local extreme value along the branch of solutions.
We will illustrate these concepts by considering
the case ![]() of the discrete strut example. The
of the discrete strut example. The ![]() case can be solved in an essentially explicit fashion, but it is a little
too simple to truly explain the perturbation expansion described above.
You will consider the case
case can be solved in an essentially explicit fashion, but it is a little
too simple to truly explain the perturbation expansion described above.
You will consider the case ![]() in the exercise session.
in the exercise session.
This n=1 strut problem will soon be available
on the web too.