Chaire d'Analyse Appliquée                    The DNA modelling COURSE

Session 7

Introduction

We finished up last session (week 5) with a discussion of the bifurcation diagram for the one degree of freedom strut example, both perturbed and un-perturbed, and in the exercises you considered the two degrees of freedom case.

Today we will briefly re-consider the $n$ degrees of freedom example, consider the limit $n\to \infty$ to recover the continuous case, do some bifurcation analysis on the continuous problem, and then describe a different discretization of the continuous problem (using collocation) that is used by the numerical continuation package AUTO.
 

The Continuous Limit

Consider first the energy of the discrete problem

$$\sum_{i=0}^n k_{i+1} (\phi_{i+1} - \phi_{i} -\beta_{i+1})^2/2 + \lambda h\, \cos\phi_{i}$$

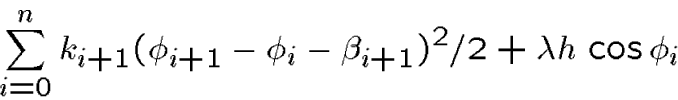
where $\lambda$, $h$, the $\beta_{i+1}$, and the $k_{i+1}$, $i=0,\dots,n$ are given, there are $n+2$ unknown variables $\phi_{i}$, $i=0,\dots,n+1$, and we have the ``boundary conditions''

$$\phi_0=\beta_0,\quadk_{n+1}(\phi_{n+1} - \phi_{n} - \beta_{n+1})=0.$$

where $\beta_0$ is an additional parameter.
 

1. Moment Balance Equation

The discrete moment balance equilibrium condition

$$\begin{align*} -k_{i+1} (\phi_{i+1} - \phi_i -\beta_{i+1}) ... ..._{i-1} -\beta_{i}) &- \lambda\,h\, \sin\phi_{i}=0\end{align*}$$

can be recognized as a simple finite difference discretization of the continuum moment balance equation in the form

$$-\left(K_2(s)(\phi'(s) - \hat u_2(s))\right)'-\lambda\sin\phi(s)=0$$

with discretization size  and $$k_i \equiv K_2(i\,h)/h,\quad \beta_i \equiv \hat u_2(i\,h)/h$$

For the extreme values of the index $i$ we also recover a finite difference discretization of the boundary conditions

$$\phi(0)=0 \quad K_2(1)(\phi'(1) - \hat u_2(1))=0$$

We can also see that the discrete energy

$$\sum_{i=0}^n k_{i+1} (\phi_{i+1} - \phi_{i} -\beta_{i+1})^2/2 + \lambda h\, \cos\phi_{i}$$

with discretization size  and $$k_i \equiv K_2(i\,h)/h,\quad \beta_i \equiv \hat u_2(i\,h)/h$$

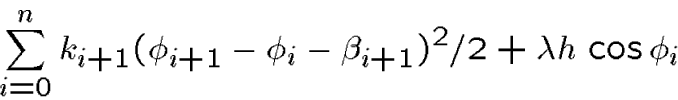
is a finite difference approximation to the the continuous energy

$$\int_0^1 K_2 (\phi'-\hat u_2)^2/2 + \lambda \cos\phi\ ds$$

(we will return to this observation in a little bit).
 

2. The Discrete Force Balance Equations

A question that we have so far ignored, is what happened to the force balance laws in our discrete variational formulation? It is reasonable that we can obtain a variational principle just in terms of the discretized angle, because for the strut problem, in the continuous version the force balance laws and the moment balance decouple.

Explicitly

$$N_1'=0,\quad N_3'=0$$ taken with the boundary conditions $$N_1(1)=0, \quad N_3(1)=-\lambda$$ imply $N_1(s)\equiv 0$ and $N_3(s)\equiv-\lambda$.

And the kinematic incompressibility and unshearability constraints and boundary conditions written in the form

$$x'=\sin\phi,\ x(0)=0,\ z'=\cos\phi,\ z(0)=0$$

(with the notation ${\bf r}(s)=x(s)\i_1 + z(s)\i_3$) allowed us to reduce the whole equilibrium problem to the solution for $\phi$ and $m_2$ of the (continuous) moment balance equation with boundary conditions and parameter$\lambda$, after which the centreline was reconstructed.

It will be instructive to describe the analogous procedure for the discretized system. The finite difference approximation to the kinematic constraint equations are for $i=1,\dots,n$

$$x_i-x_{i-1}=h\,\sin\phi_{i-1},\ x_0=0$$
$$z_i-z_{i-1}=h\,\cos\phi_{i-1},\ z_0=0$$

And the appropriate discretized variational principle is to `minimize' the elastic potential energy in the form

$$\sum_{i=0}^n k_{i+1} (\phi_{i+1} - \phi_{i} -\beta_{i+1})^2/2 + \lambda z_n$$

subject to the same boundary conditions as before $$\phi_0=\beta_0,\ k_{n+1}(\phi_{n+1} - \phi_{n} -\beta_{n+1})=0.$$

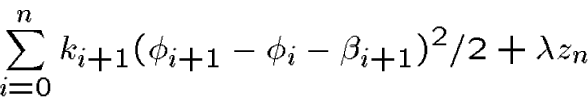
but now also subject to the discretized kinematic constraints (and boundary conditions).

For such a finite dimensional constrained variational principle we have (at least formally) a Lagrange multiplier rule: to each constraint we can associate a Lagrange multiplier, say $\nu_i$ and $\mu_i$, $i=1,\dots,n$, and constrained critical points will satisfy the first-order conditions for the function

$$\begin{align*}\sum_{i=0}^n k_{i+1}(\phi_{i+1} &-& \phi_{i} ... ...1}(z_{i+1}-z_{i}-h\,\cos\phi_{i})\\ &+ \lambda z_n\end{align*}$$

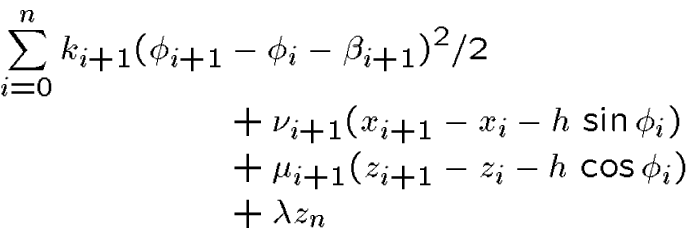
with respect to the unknowns $\phi_{i}$, $x_i$ and $z_i$ treated as independent variables (i.e. ignoring the constraint equations) for some values of the multipliers $\nu_i$ and $\mu_i$. For consistency here we set $\nu_{n+1}=\mu_{n+1}=0$ because there are only $2n$ constraints, and $2n$ unknowns $x_i$ and $z_i$.

 The first-order conditions with respect to $x_i$ and $z_i$ yield the system of equations

$$-\nu_{i+1}+\nu_{i}= 0,\quad i=1,\dots,(n-1),\quad \nu_n=0,$$ and $$-\mu_{i+1}+\mu_{i}= 0,\quad i=1,\dots,n-1,\quad \mu_n = -\lambda$$

which can be recognized as finite difference approximations to the two force balance equations, and their associated boundary conditions.

Just as in the continuous case it is trivial to solve the force balance conditions, and we obtain

$$\nu_i= 0,\quad \mu_i=-\lambda,\quad i=1,\dots,n$$

For the full variational principle, the first-order conditions for the $\phi_{i}$ regarded as being completely independent of the $x_i$ and$z_i$, are

$$\begin{align*} -k_{i+1} (\phi_{i+1} - \phi_i -\beta_{i+1}) ... ...\, \sin\phi_{i}\\ &-\nu_{i+1}\,h\, \cos\phi_{i}=0.\end{align*}$$

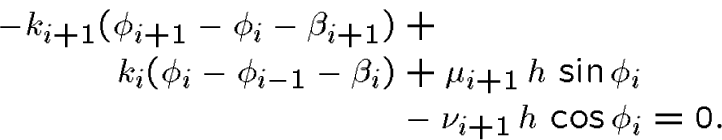
And when we use the closed form expression to eliminate the multipliers, we re-obtain the first-order necessary conditions for the variational principle involving the angles only.

It should be noted that the strut boundary value problem is very special. Just about every piece of the problem enters in just the right way for this decoupling to arise. For different boundary conditions, or a $z$ dependent potential term the problem remains coupled.

Nevertheless in general a variational principle is possible whenever the constitutive relations are hyper-elastic. The variational principle involves minimizing the internal elastic energy (or the integral of the strain energy density function) plus any additional potential terms which arise from end-loadings say, and subject to some set of imposed boundary conditions and constraints.

Exercise: Construct the variational principle for the strut boundary value problem (i.e. the same boundary conditions and end-loading), but now for a rod that has a diagonal shearable, extensible constitutive relation.
 

A Little Bifurcation Theory For The Continuous Problem

Recall that the equilibrium conditions are

$$N_1'= 0\, ,\qquad N_3'= 0,\quad N_1(1)=0, \quad N_3(1)=-\lambda$$

$$[K_2(s)(\phi'-\hat u_2(s))]'= N_3\,\sin \phi - N_1\,\cos \phi$$

$$\phi(0)=0 \quad K_2(1)(\phi'(1) - \hat u_2(1))=0$$

$$x'=\sin\phi,\ x(0)=0,\ z'=\cos\phi,\ z(0)=0$$

When does this system have a singular Jacobian? Or in other words if we linearize about a known solution, when can the resulting linear system have a non-trivial solution?

In general this is a different calculation for each known solution. We have two possibilities. First when $\lambda =0$ we have the unstressed shape.

Exercise: Verify that the linearization at the unstressed shape is always nonsingular so that (assuming the appropriate infinite dimensional version of the implicit function theorem), there is locally a unique branch of solutions through the zero load configuration.

The second possibility is that when $\hat u_2(s)\equiv 0$, there is the upright straight solution for all $\lambda$, and we can linearize about each of those solutions. Motivated by the discrete problem we would anticipate finding $\lambda$ values when there are non-trivial solutions (i.e. the Jacobian is singular). This can be shown to be true explicitly in the further special case $K_2(s)\equiv 0$ by calculating the sequence of $\lambda_j$, $j=1,\,2,\dots$, called bifurcation points or buckling loads, at which the Jacobian is singular.

It can be shown that a countable sequence of $\lambda_j$,$j=1,\,2,\dots$ of bifurcation points actually exists for any$K_2(s)\gt$, and you can estimate their location analytically, but you cannot (in general) find them explicitly. (This is the theory of ODE called spectral theory for Sturm-Liouville operators.) We will also return to this problem in a little while.

Of course we can numerically compute the bifurcation points to any reasonable accuracy with a good code.
 

The Collocation Discretization

We will discretize using (Gaussian) collocation. Roughly speaking this means approximating each unknown function by a continuous piece-wise polynomial of a specified degree (say 3 or 4 or 5) on a given number of sub-intervals (say 20 or 30).

When a function is approximated by a piece-wise polynomial, its derivative in the interior of the sub-intervals is also approximated, merely by differentiating the piece-wise polynomial. We get a finite dimensional system of equations to solve for the coefficients of the piece-wise polynomial merely by enforcing the differential equation at an appropriate number of interior points in each sub-interval.

Of course there is a big numerical analysis theory of collocation, giving error bounds and identifying the `best' points at which to collocate (the Gaussian quadrature points of course!)

Collocation can be viewed as being intermediate between finite difference and finite element discretizations. For example piecewise linear collocation is simply related to first order differencing of derivatives. While collocation can also be viewed as a finite element method where the trial functions are piece-wise polynomial, and the test functions are Dirac deltas (centred on the collocation points).

For our later purposes Gaussian collocation is very nice because it can be shown to be equivalent to a symplectic Runge-Kutta method (say marching in from the left) for the values of the functions at the boundaries between sub-intervals. And when the underlying equations are Hamiltonian, symplectic R-K methods exactly conserve the value of any integrals of the continuous Hamiltonian system that are quadratic functions of the unknowns (ie the phase variables).
 

VBM and AUTO

The package AUTO implements collocation (even with an adapting mesh), exploits special linear algebra for the sparsity structure of the Jacobian associated with the collocation discretization, and has routines both for continuing around fold points in a branch of solutions, and for switching branches at bifurcation points.

As with any large code you must use AUTO with caution, until you get to know its strengths and limitations.

For example bifurcation points arise when the Jacobian is singular, but it is computationally expensive to monitor singularity. So AUTO tracks the sign of the determinant. This is much faster, and most of the time catches points where the Jacobian is singular. However in the atypical case that the Jacobian has a double zero eigenvalue, the Jacobian can go singular without the determinant vanishing and AUTO typically misses any such bifurcation points.

There are several other trade-offs between speed in the typical case, and robustness to even the most degenerate case, which can give misleading answers when the atypical cases happen to arise.

The resolution is to go ahead and use the code, but always to be questioning and testing it to the full extent possible.

Generally our experience is that AUTO is pretty robust.

VBM is an ``easy to use'' interface to AUTO that has two modes. (In fact VBM is designed to be coupled to many different continuation packages, but we will only use AUTO.)

The post-processing mode allows one to use interactive visualization to understand bifurcation diagrams, and particular solutions on the bifurcation diagram that have already been computed.

The computation mode allows you to interactively extend bifurcation diagrams through additional computations using AUTO.

In point of fact the planar strut examples you will see today are so simple that they don't really justify all the overhead you have to learn to use VBM. However the objective is to learn and build confidence in VBM/AUTO before using it in the three dimensional rod examples that we will use to model DNA.
 

Back to the Table of Contents
12/15/1998