Basic usage example¶
We will solve the following system 1
where \(t \in [0,1]\) and \(y(0) = 0\).
First we must write the problem definition. It is rather long so it is not included here but on a separate page. Some methods of the BVPSolution class and some extra methods were used to help define the system.
Copy the problem definition and save it as test_system.py. We will solve the system for \(\alpha = 5\). First, import the necessary modules, including the problem definition, and setup the problem.
import numpy as np
from test_system import DAE
from daepy import BVP
from matplotlib import pyplot as plt
alpha = 5
dae = DAE(alpha)
Next we create a BVP class and give it an initial guess for the solution, in this case \(y(t) = 0\).
degree = 3
intervals = 10
bvp = BVP(dae, degree, intervals)
bvp.initial_guess([lambda x: 0], initial_interval=[0,1])
Now we can solve the system.
sol = bvp.solve(method='nleqres', tol=1e-14, maxiter=100, disp=True)
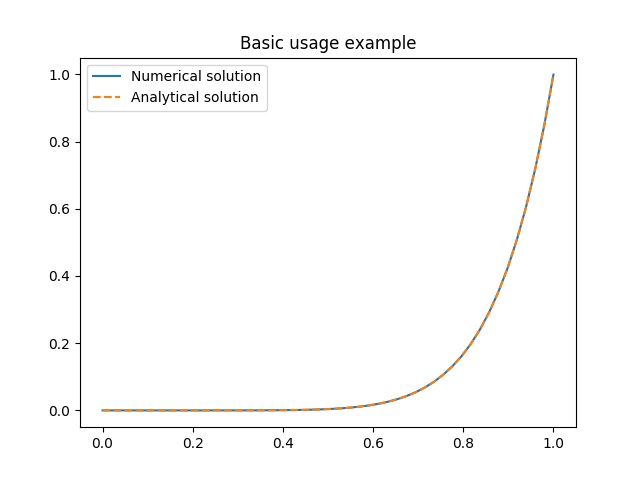
Finally, we can plot the solution against the known analytic solution \(y(t) = t^{3+\alpha}\).
l = np.linspace(0,1)
plt.plot(l, sol.eval(l))
plt.plot(l, l**(3+alpha), '--')
plt.legend(['Numerical solution', 'Analytical solution'])
plt.title('Basic usage example')
plt.show()
This should produce a plot like this.
Parameter continuation example¶
We will solve the same system as in the basic usage example but this time for \(\alpha\) from 10 to 50 using parameter continuation. The setup is the same as before.
import numpy as np
from test_system import DAE
from daepy import BVP
from matplotlib import pyplot as plt
alpha = 10
dae = DAE(alpha)
degree = 3
intervals = 20
bvp = BVP(dae, degree, intervals)
bvp.initial_guess([lambda x: 0], initial_interval=[0,1])
Now we define a callback function which will plot the solution at each continuation step.
def callback(p, sol):
colour = (min((p-10)/40, 1.0), 0.0, max(1-(p-10)/40, 0.0))
l = np.linspace(0,1)
plt.plot(sol.forward(l), sol(l), color=colour) # plot using internal coordinate for smoother lines
Now can perform the parameter continuation.
steps = list(range(15,51,5))
bvp.continuation(alpha, method='pseudo_arclength', steps=steps, tol=1e-14, maxiter=100, disp=True, callback=callback)
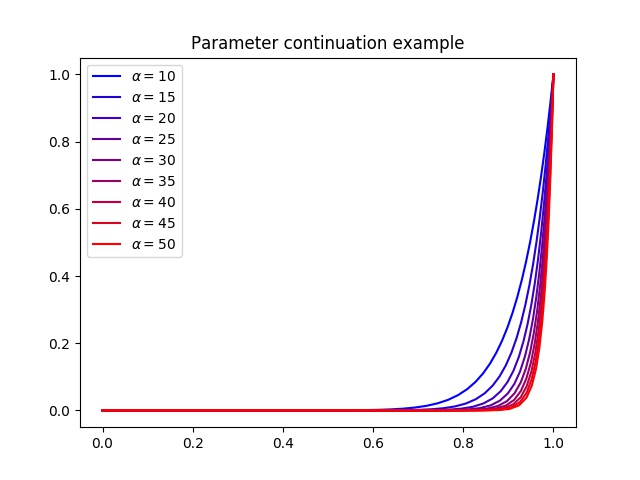
In this example we gave the continuation steps explicitly as a list but it is also possible to just give a number of steps and a target value for the parameter. Finally, we show the plot we have made.
plt.legend([r'$\alpha = $' + str(s) for s in [alpha] + steps])
plt.title('Parameter continuation example')
plt.show()
This should produce a plot like this.
- 1
Tavernini, The Approximate Solution of Volterra Diff. Systems with State-Dependent Time Lags, SIAM J. Num. Anal. Vol. 15 (1978). 1039-1052